SVM is one of the most popular, versatile supervised machine learning algorithm. It is used for both classification and regression task.But in this thread we will talk about classification task. It is usually preferred for medium and small sized data-set.
The main objective of SVM is to find the optimal hyperplane which linearly separates the data points in two component by maximizing the margin .
Don’t panic with the word ‘hyperplane’ and ‘margin’ that you have seen above. It is explained in details below.
Points to be covered:
1. Basic linear algebra
2. Hyper-plane
3. What if data points is not linearly separable ?
4. Optimal Hyperplane
5. How to choose optimal Hyperplane ?
6. Mathematical Interpretation of Optimal Hyperplane
7. Basic optimization term
8.SVM Optimization
Basic Linear Algebra
Vectors
Vectors are mathematical quantity which has both magnitude and direction. A point in the 2D plane can be represented as a vector between origin and the point.

Length of Vectors
Length of vectors are also called as norms. It tells how far vectors are from the origin.

Direction of vectors
Direction of vector .
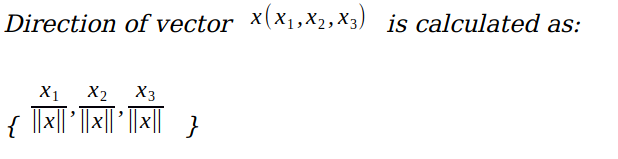
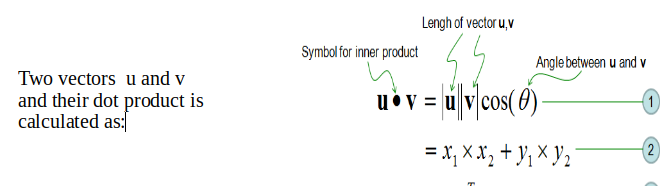
Dot Product
Dot product between two vectors is a scalar quantity . It tells how to vectors are related.
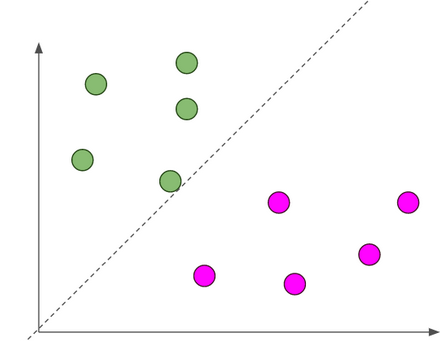
Hyper-plane
It is plane that linearly divide the n-dimensional data points in two component. In case of 2D, hyperplane is line, in case of 3D it is plane.It is also called as n-dimensional line. Fig.3 shows, a blue line(hyperplane) linearly separates the data point in two components.
In the Fig.3, hyperplane is line divides data point into two classes(red & green), written as

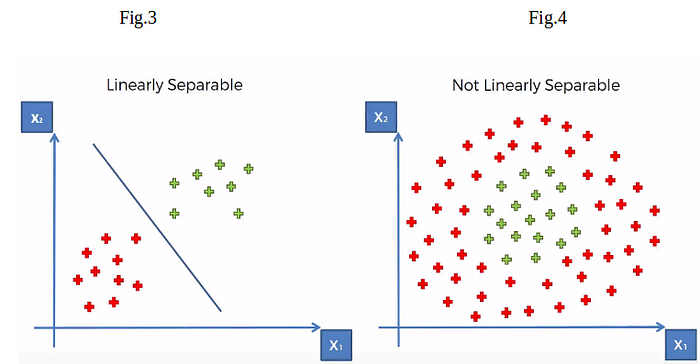
What if data points is not linearly separable ?
Look Fig.4 how can we separate the data-points linearly? This type of situation comes very often in machine learning world as raw data are always non-linear here.So, Is it do-able? yes!!. we will add one extra dimension to the data points to make it separable.
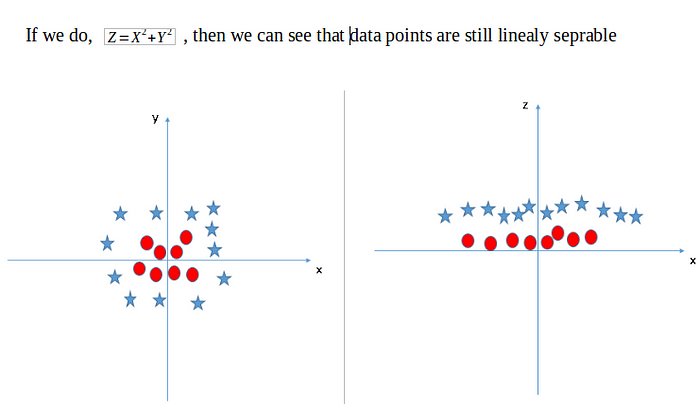
so , the above process of making non-linearly separable data point to linearly separable data point is also known as Kernel Trick, which we will cover later in details.
Optimal Hyperplane
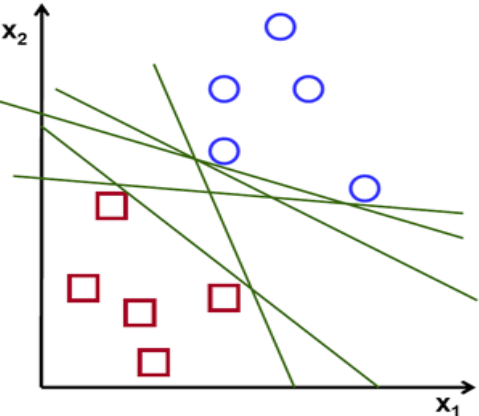
If you look above Fig there are numbers of hyperplane that can separate the data points in two components. So optimal hyperplane is one which divides the data points very well. So question is why it is needed to choose optimal hyper plane?
So if you choose sub-optimal hyperplane, no doubt after number of training iteration , training error will decrease but during testing when an unseen instance will come, it will result in high test error. In that case it is must to choose an optimal plane to get good accuracy.
How to choose Optimal Hyperplane ?
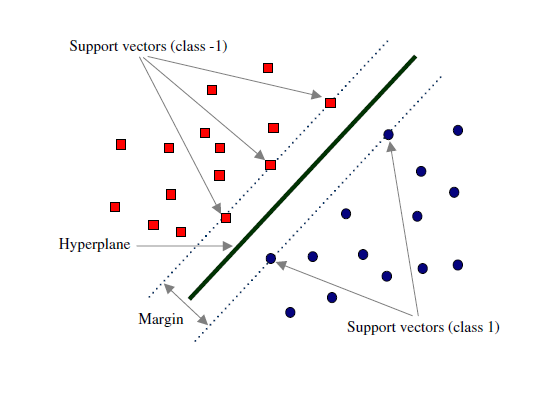
Margin and Support Vectors
Let’s assume that solid black line in above Fig.7 is optimal hyperplane and two dotted line is some hyperplane, which is passing through nearest data points to the optimal hyperplane. Then distance between hyperplane and optimal hyperplane is know as margin, and the closest data-points are known as support vectors. Margin is an area which do not contains any data points. There will be some cases when we have data points in margin area but right now we stick to margin as no data points lands.
So, when we are choosing optimal hyperplane we will choose one among set of hyperplane which is highest distance from the closest data points. If optimal hyperplane is very close to data points then margin will be very small and it will generalize well for training data but when an unseen data will come it will fail to generalize well as explained above. So our goal is to maximize the margin so that our classifier is able to generalize well for unseen instances.
So, In SVM our goal is to choose an optimal hyperplane which maximizes the margin.
— — — — — — —
Since covering entire concept about SVM in one story will be very confusing. So i will be dividing the tutorial into three parts.
- Linear separable data points.
- Linear separable data points II.
- Non-linear separable data-points.
So, In this story we will assume that data points(training data) are linearly separable.Lets start,
Mathematical Interpretation of Optimal Hyperplane
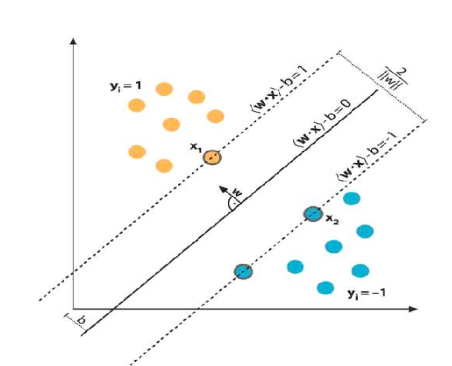
we have l training examples where each example x are of D dimension and each have labels of either y=+1 or y= -1 class, and our examples are linearly separable. Then, our training data is form ,
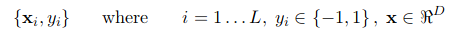
We consider D=2 to keep explanation simple and data points are linearly separable, The hyperplane w.x+b=0 can be described as :
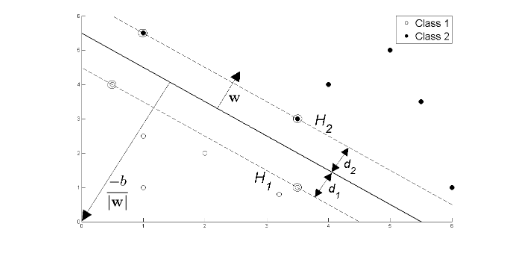
Support vectors examples are closest to optimal hyperplane and the aim of the SVM is to orientate this hyperplane as far as possible from the closest member of the both classes.
From the above Fig , SVM problem can be formulated as,

From the Fig.8 we have two hyperplane H1 and H2 passing through the support vectors of +1 and -1 class respectively. so
w.x+b=-1 :H1
w.x+b=1 :H2
And distance between H1 hyperplane and origin is (-1-b)/|w| and distance between H2 hyperplane and origin is (1–b)/|w|. So, margin can be given as
M=(1-b)/|w|-(-1-b)/|w|
M=2/|w|
Where M is nothing but twice of the margin. So margin can be written as 1/|w|. As, optimal hyperplane maximize the margin, then the SVM objective is boiled down to fact of maximizing the term 1/|w|,

Basic optimization algorithm terms
Unconstrained optimization
Example will be more intuitive in explaining the concept,
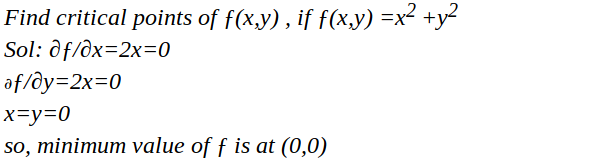
So, it is same that we used to do in higher school in calculus for finding maxima and minima of a function. Only difference is at that time we were calculating for univariate variable, but now we are calculating for multivariate variables.
Constrained optimization
Again it will become clear with an example,

So basically we calculate the maxima and minima of a function by taking into the consideration of given constraints on the variables.
Primal and Dual Concept
Shocked!! what the heck is this now???
Don’t worry, it ‘s theory only !!
Lets not get deep into these concept. Any optimization problem can be formulated into two way, primal and dual problem. First we use primal formulation for optimization algorithm, but if it does not yield any solution, we go for dual optimization formulation, which is guaranteed to yield solution.
Optimization
This part will be more mathematical, some terms are very high level concept of mathematics, but don’t worry i will try to explain each one by one in layman term.
To make you comfortable, Learning algorithms of SVM are explained with pseudo code explain below. This is very abstract concept in SVM optimization. For below code assume x is data point and y is its corresponding labels.

Just above you see learning process of SVM. But here is a catch, how do we update w and b ??
Gradient descent of course!!! — -BIG ‘NO’.
why not Gradient descent??
SVM optimization problem is a case of constrained optimization problem, and it is always preferred to use dual optimization algorithm to solve such constrained optimization problem. That’s why we don’t use gradient descent.
Since it is constrained optimization problem Lagrange multipliers are used to solve it, which is described below, It looks like , will be more mathematical but it is not, its just few steps of finding gradient. We will divide the complete formulation into three parts.
- In first we will formulate SVM optimization problem Mathematically
- we will find gradient with respect to learning parameters.
- we will find the value of parameters which minimizes ||w||

The above equation is Primal optimization problem.Lagrange method is required to convert constrained optimization problem into unconstrained optimization problem. The goal of above equation to get the optimal value for w and b.

May be above equation is looking tricky? but it is not, its just high school math of finding minima with respect to variable.
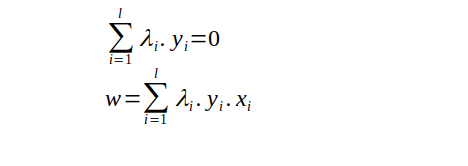
As,from the above formulation we only able to find the optimal value of w and that is to dependent on λ, so we need to find the optimal value of λ also. And finding optimal value of b needs both w and λ. So finding the value of λ will be the important for us.
so how do we find the value of λ???
Above formulation is itself a optimization algorithm, but it not helpful to find the optimal value. It is primal optimization problem. As we read above that if Primal optimization doesn’t result in solution, we should use dual optimization formulation, which has guaranteed solution. Also when we move from primal to dual formulation we switch minimizing to maximizing the loss function. Again we will divide the complete formulation into three parts to easier to understand.
- Problem formulation and substitution value from primal
- Simplify the loss function equation after substitution
- final optimization formulation to get the value of λ
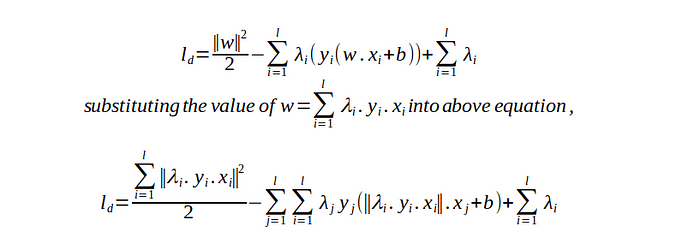
Above equation is a dual optimization problem. The equation are looking scarier because of substitution of value of w.

It is simplified equation of above dual optimization problem.
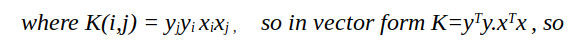

So this is the final optimization problem, to find the maximum value of λ. Here one more term K is there, which is nothing but dot product of input variable x. (This K will be very important in future when we will learn about kernel trick and non-linear data points).
Now How do we Solve the above problem??
Above maximization operation can be solved with the SMO ( sequential minimization optimization) algorithms . There are also the various library support online for this optimization. Once we get the value of λ we can get w from below equation
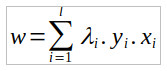
and using value of w , λ we will calculate b as following,

As we now have the value for both w and b , then optimal hyperplane that can separates the data points can be written as,
w.x + b = 0
And a new example x_ can be classified as sign(w.x_ +b)
Thanks for reading, this is the PART1 of SVM, in PART 2 we will discuss about how to deal with a case when data is not fully linearly separable.
